Pattern Formation in Chemistry
Pattern Formation in Chemistry
Visualization of the dynamics of reactive solutions
Formation and decay of complex structures is a characteristic property of matter in the universe. Life on earth presents impressive examples. Over the past decades, theoretical as well as experimental research has shown that the formation of diverse spatial patterns is based on nonlinear interactions between transport and chemical modification of matter.
One approach to a deeper understanding of the intricate dynamics of such phenomena is the investigation of fundamental processes in the laboratory. Two processes have been very fruitful here: the oxidation of malonic acid in the presence of bromo compounds, called Belousov-Zhabotinskii reaction in honor of its discoverers, and the degradation of sugar in cellular cytoplasm, glycolysis.
The dynamic formation of spatial patterns in such systems may be observed with
a two-dimensional spectrophotometer. This apparatus contains a video camera which records the intensity levels in a monochromatic field of light which has passed through a chemical solution. The signals recorded by the camera are digitized, transferred to a computer and stored in a data-array for further processing. From the intensity of light, the concentration of chemical reagents in the solution can be calculated.
All of the pictures C1 through C25 are visualizations of two-dimensional data arrays consisting of some 200.000 pixels. Appropriate interpolation algorithms render a relief of concentration, a surface in three-dimensional space, if the concentration measured in a thin solution layer is correlated to the third dimension of a coordinate system. Through computer graphics, the whole relief or any detail may be displayed on a video monitor from any desired viewpoint. In this way, chemical gradients are made visible in perspective.
Modern color monitors offer many ways to choose among numerous correlations between intensity and color. Color is particularly suited to emphasize the slightest differences in intensity. Most interesting are those choices of form and color which appeal to the aesthetic sense of the observer. Much to our surprise, scientific information and attractive graphical design often join in a way which inspires the creativity and imagination of the scientist.
Stefan C. Müller and Theo Plesser
Experimentally observed chaotic patterns, caused by interaction of chemical waves (Belousov-Zhabotinskii reaction) with convective flow, which is induced by evaporation.
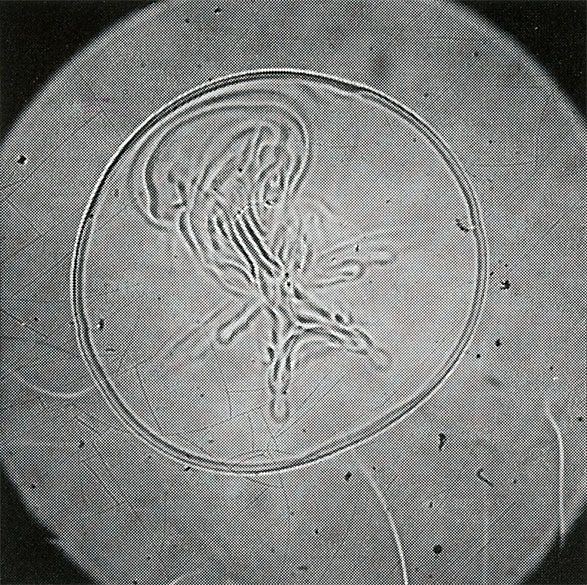
Spiral waves, which evolved from the state shown in image C1 by self-organization after evaporation had been prevented. Similar patterns can be observed in slime molds, the flickering heart muscle, and the retina (compare M15 and C5).
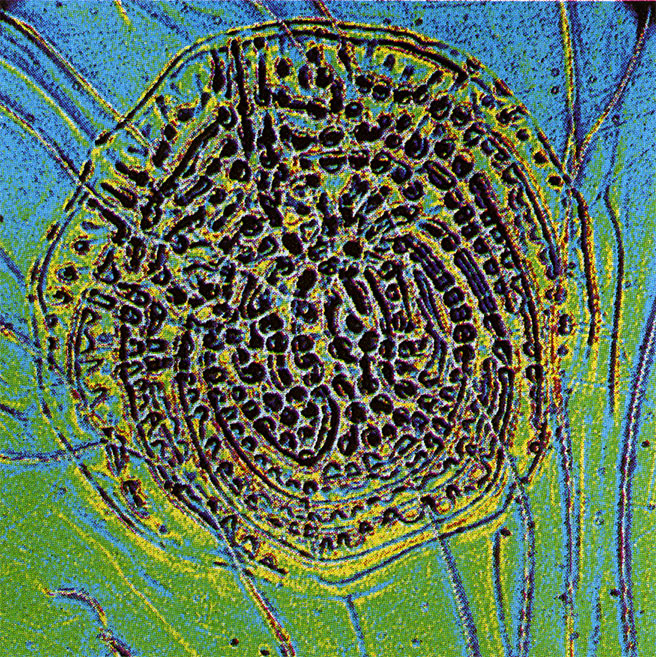
Among the fascinating abundance of shapes in nature, the spiral stands out as a widespread structural element. Think of the form of snail-shells, of the order of sunflower kernels, of hurricane funnels or of distant galaxies. In aqueous solutions, chemical reactions may also develop spiral-shaped patterns, as the chemical waves in the Belousov-Zhabotinskii reaction show.
This picture with its relief structure is based on a chemical spiral which rotates around a center and at the same time expands two-dimensionally within a thin layer of solution. The distance between two wave-fronts is about 1 mm.
Precise measurement of the center of rotation — located at the inner side of the spiral tip (C4) — and analysis of lines of equal concentration (C5) reveal that the geometry of the wave develops according to the rules of an Archimedian spiral.
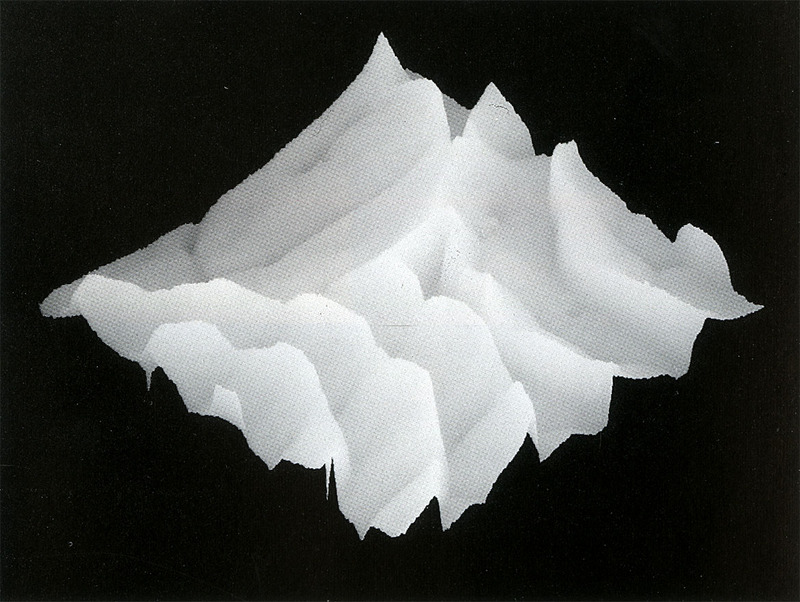
The spiral wave observed in the Belousov-Zhabotinskii reaction turns around the center of rotation once every eighteen seconds. Thus, a sequence of six images taken in three second intervals covers exactly one rotation. Since all images are stored as digital data arrays, they can be superimposed in a way such that at every single point of the image only the maximum concentration measured will be displayed. Through this technique, an important feature of chemical spiral-structures is visualized within a single image — the wave-amplitude declines towards the spiral center. A 'concentration well" is formed, which remains steady at its center by interaction of diffusion and reaction. Picture C6 shows the spiral core in 3D perspective, where the viewpoint of the observer is located above the concentration maxima.
This image was recorded and processed in the same way as C6, but now a larger part of the solution was observed with the camera, so that several spirals are measured. The three-dimensional perspective from "below" visualizes the envelopes of the deep "concentration wells" around the rotation centers. They demonstrate the singular character of the chemical processes in the core areas and resemble the shape of tornados very closely.
The cone shows a spiral core, which can be generated from the same data used for the production of image C6. By reflection with respect to the plane of the concentration maxima, this core is transformed into a "monument," rising on a pedestal formed of spirals.
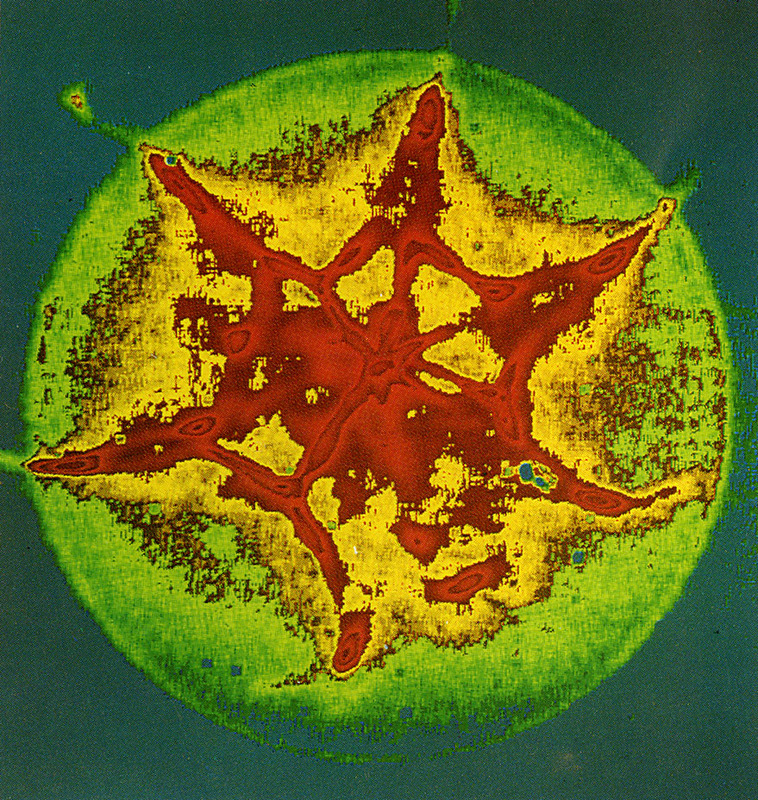
Complex patterns of concentration occur where several spiral-shaped fronts propagating in different directions collide. Picture C9 is a snapshot visualization of chemical gradients observed in such patterns, as they move through the solution in a perfect balance of reaction and diffusion. This demonstrates that geometrically simple and sharply defined structures may, in fact, exist in liquid phase, like a chemically reactive aqueous solution.
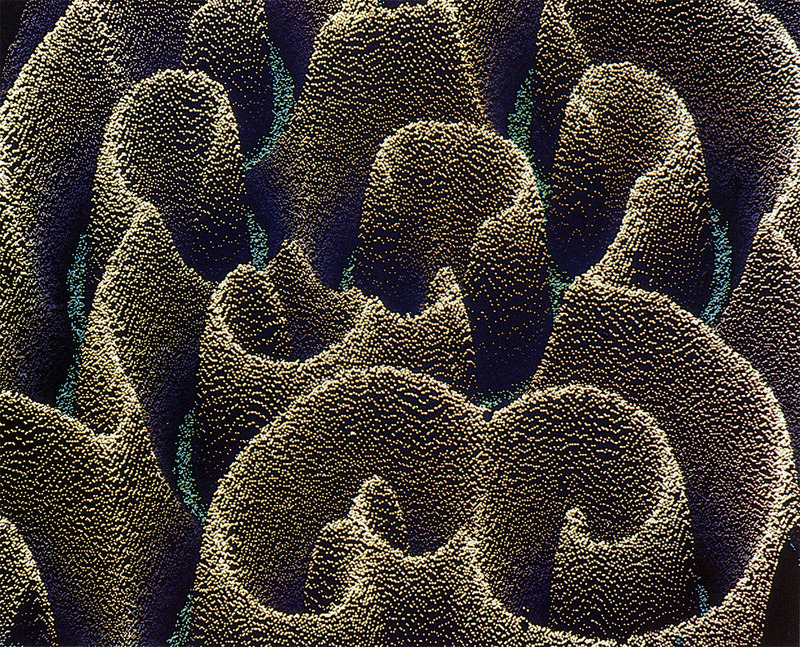
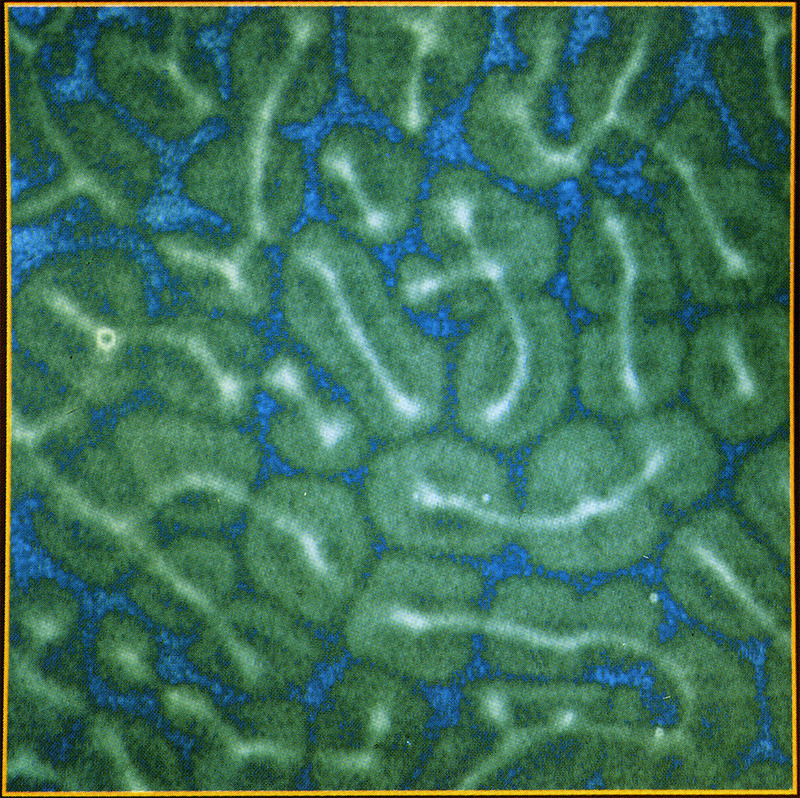
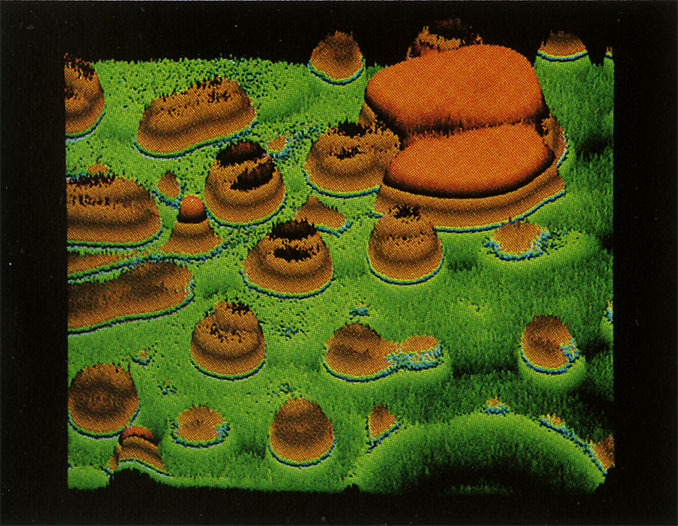
The dynamics of pattern formation reaches a higher level of complexity as soon as convective flow joins diffusion as a transport mechanism. If, e.g., surface forces, as they are caused by gradients in concentration and/or temperature (mostly induced by evaporation), get off balance, the lower layers of the solution often arrange themselves in surprisingly regular patterns in the millimeter range. The bright and dark lines in the picture mark the boundaries of so-called convection cells, where streams of the liquid moving in different directions encounter. In these regions the mixing of substances is more pronounced and therefore matter transport is increased, “stimulating” the chemical reaction, as shown in picture C18.
The subsequent series of pictures (C14—C22) gives an impression of the effects which convection may exert on the Belousov-Zhabotinski reaction (BZ) as well as on cell-free cytoplasm of yeast in which metabolic turnover takes place.